개념

집합: 순서와 중복이 없는 원소들을 갖는 자료구조

집합의 종류

특성에 따라 부르는 말이 다양합니다.

수학적으로는 더 많은 집합들이 있겠지만 상호배타적 집합에 집중해봅시다.

상호배타적 집합

교집합이 없는 집합 관계

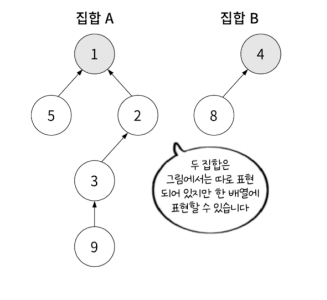
위 그림은 A=3, B=7을 나타낸 그림입니다. A와 B는 겹치는 원소가 없으므로 교집합이 없다고 볼 수 있죠.

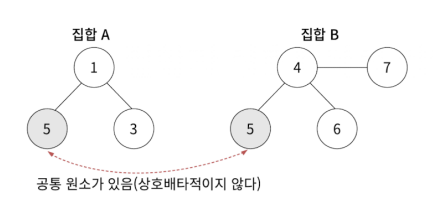만약 공통 원소가 있으면 상호배타적 집합에 해당하지 않아요.

활용 분야

흔히 코딩 테스트에서는 그래프 알고리즘에서 상호배타적 집합을 많이 활용합니다. 사이클을 확인할 때 상호배타적인지를 확인하면 되기 때문이죠. ( 무방향 그래프에서만 해당합니다. )

이외에도 다음과 같은 활용도가 있어요.

1. 이미지 분할: 사람과 배경의 구분
2. 도로 네트워크 구성: 도로가 교차하지 않도록 설계
3. 최소 신장 트리 알고리즘: 간선을 추가할 때 사이클 형성 여부 체크
4. 게임 개발: 플레이어와 적군이 충돌할 때 겹치지 않도록 구분
5. 클러스터링 작업: 작업이 겹치지 않도록 구성

구현

보통 집합은 트리로 표현되며 대표적인 연산은 Union과 Find가 있습니다. 우선 집합을 어떻게 표현하는지부터 살펴봅시다.

배열을 활용한 트리로 집합 표현

배열을 활용하여 집합을 표현하기 위해선 각 집합에 대표 원소가 있어야 합니다.

대표 원소

집합의 원소 중 집합을 대표하는 역할 개념적으로 집합의 대표 원소와 트리의 루트 노드는 같다.

하나의 배열에 집합을 모두 표현하려면 다음의 법칙을 따라야 합니다.

• 배열의 인덱스는 자신, 배열값은 부모 노드를 의미한다.

예를들면 set[3] = 9 라면 노드 3의 부모는 9임을 의미하는 것이죠. 루트 노드의 경우에는 부모가 없기에 본인의 인덱스를 그대로 값으로 내려줍니다.

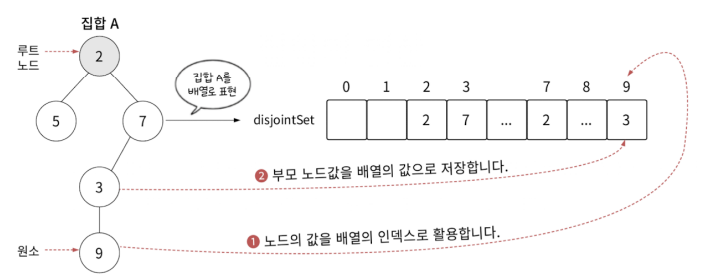
이렇게 되면 자연스럽게 배열의 최소 크기는 원소 중에서 가장 큰 값보다 1 큰 값이 됩니다.

예시

루트 노드만 잘 관리하면 여러 개의 집합을 하나의 배열로 표현할 수 있게 됩니다. (집합의 개수는 루트 노드의 개수)

구현 과정

1. 초기 상태

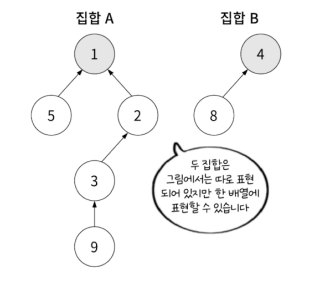
초기 상태는 자기 자신을 루트 노드로 설정한 상태입니다. 집합에 없는 인덱스의 값은 -1로 임의로 정해봅시다. 아래 집합 부분과 같이 각 원소들이 전부 루트 노드로 표현되고 있어요. ( 인덱스와 값이 같음 )

2. 집합 연결

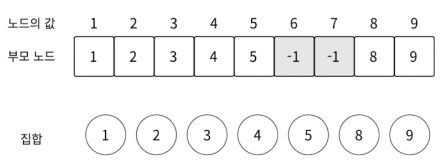
주어진 집합을 기준으로 적용하면 위와 같이 구성됩니다. 만약 노드 9가 루트 노드가 1인 집합 A에 속하는지 루트 노드가 4인 집합 B에 속하는지 확인하려면 set[9]=3 set[3]=2 set[2]=1 set[1]=1의 방향으로 탐색하면 돼요.

집합 자체를 주로 어떤 방식으로 구현하는지 확인해봤습니다. 이제 이 집합으로 어떤 연산을 하는지 확인해봅시다.

유니온-파인드 알고리즘

union-find algorithm

집합 알고리즘에 주로 쓰이는 연산은 합치기(union)와 탐색(find)입니다.

find

특정 노드의 루트 노드가 무엇인지 탐색하는 방법

특정 노드부터 재귀로 거슬러 올라가며 루트 노드를 찾습니다.

1. 현재 노드의 부모 노드를 확인
2. 확인하다가 부모 노드가 루트 노드면 찾기 연산 종료

예시를 들어봅시다. 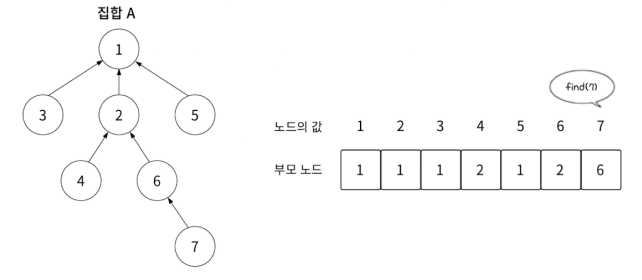find(7)로 노드 7의 루트 노드를 찾아봅시다.

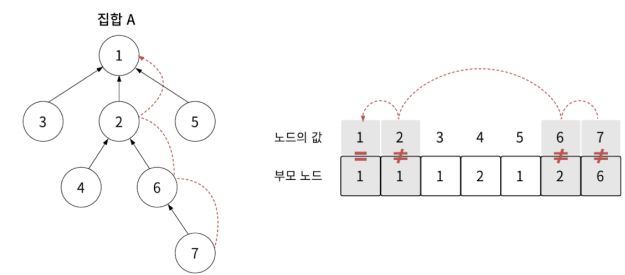값을 인덱스로 바꾸면서 부모 노드로 올라가는 과정을 거치면서 값과 인덱스가 같은 노드(루트 노드)가 나올 때까지 반복해줍니다. find(7)은 다음의 과정을 거쳐서 루트 노드를 찾게 됩니다.

set[7] = 6;
set[6] = 2;
set[2] = 1;
set[1] = 1; // 값과 인덱스가 같음 ( 찾음 )

하지만 이는 최악의 경우의 시간 복잡도가 O(N)입니다. 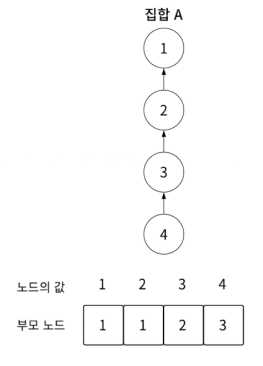좀 더 최적화하기 위해 경로 압축을 활용할 수 있습니다.

경로 압축

효율적인 find 연산을 위해서는 집합 형태를 유지하면서도 트리 높이를 줄이는 방식을 사용하면 됩니다.

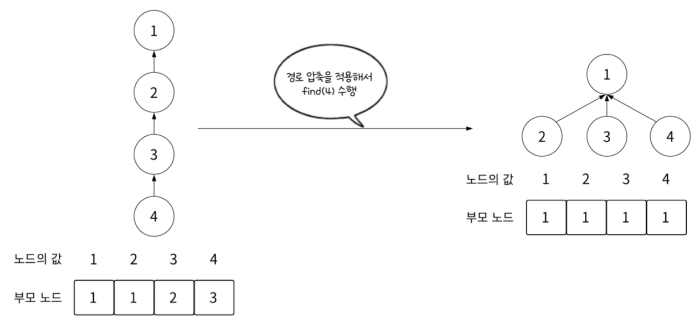
파인드 연산이 목표로 하는 것은 루트 노드를 찾는 것이기에 루트 노드만 넣어둬서 최적화하는 방식인 것이죠.

Union

두 집합을 하나로 합치는 연산, 두 집합의 루트 노드를 같게 만드는 것입니다.

1. 두 집합에서 find 연산을 통해 루트 노드를 찾습니다.
2. 찾은 두 루트 노드의 값을 비교합니다.
3. 두 집합을 합칩니다. (두 집합의 루트 노드를 같게 만듭니다.)

두 집합이 있다고 했을 때

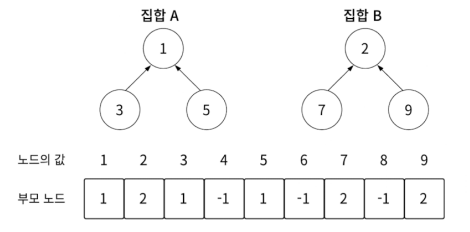
find 연산으로 두 집합의 루트 노드를 찾은 후에

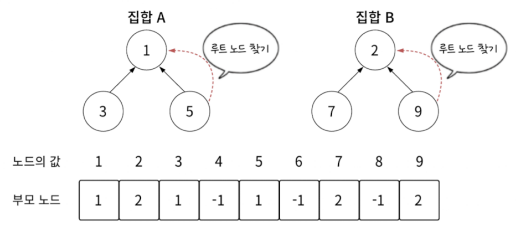
집합 A의 루트 노드 1을 루트 노드로 지정하고 집합 B의 루트 노드 2를 그 자식으로 두면 집합을 하나로 만들 수 있어요.

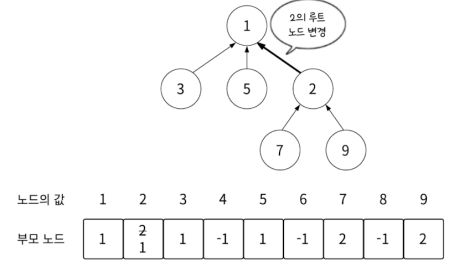
하지만 Union 연산은 트리의 깊이가 깊어지면 깊어질수록 연산 비용이 커진다는 단점이 있습니다.

이를 해결하기 위해 랭크 라는 개념을 도입할 수 있어요.

랭크

현재 노드를 기준으로 하였을 때 가장 깊은 노드까지의 경로 길이

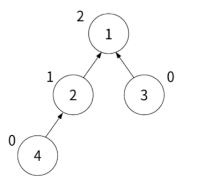
랭크를 기반으로 Union 연산을 진행하면 다음과 같은 과정을 거쳐요.

1. 두 노드의 루트 노드를 구해요. ( find )
2. 루트 노드의 랭크를 다음의 논리로 비교합니다..
   1. 랭크값이 다르면 랭크값이 더 큰 루트 노드를 작은 루트 노드의 부모 노드로 바꿉니다. ( 트리의 깊이는 더 깊어지지 않는다. )
   2. 랭크값이 같으면 루트 노드를 아무거나 선택해서 바꾸고 최종 루트 노드의 랭크에 1을 더합니다.

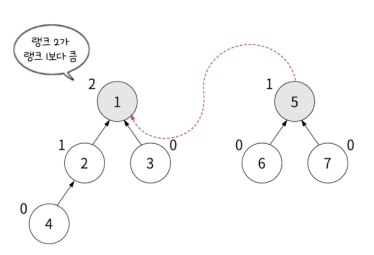
그림으로 설명해보면 두 집합이 있을 때

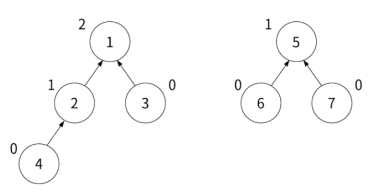
집합 A의 루트 노드 1의 랭크 2 와 집합 B의 루트 노드 5의 랭크 1을 비교합니다. 집합 A가 랭크가 더 크기 때문에 앞서 설명한 논리 1번에 의해서 집합 A의 루트 노드를 부모로, 집합 B의 루트 노드를 자식으로 연결하고 랭크는 바꾸지 않습니다.

참고 문헌

https://product.kyobobook.co.kr/detail/S000213641007

SUMMARY

알고리즘은 꾸준히 공부해주지 않으면 개념들이 유독 빠르게 사라지는 것 같아요. 사라지면 다시 채워넣을 수 있도록 꾸준히 공부해보겠습니다. 잘못된 지식이 있다면 댓글 부탁드려요!

읽어주셔서 감사해요.