data-structure

javascript

트리

2025-06-21

JS의 트리에 대해서 알아보자.

트리는 데이터를 저장하고 탐색하기에 유용한 구조를 갖고 있습니다. 계층 구조로 표현하고자 할 때 많이 사용되는데요. 같이 알아봅시다.

트리가 활용되는 분야

인공지능: 인공지능의 판단 기준을 만들 때 의사 결정 트리를 사용합니다.

자동 완성 기능: 문자열 처리에도 트리가 많이 활용됩니다. 검색 엔진에서도 자동 검색어 추천 기능도 trie라는 트리 구조를 활용합니다.

데이터베이스: 데이터를 쉽게 검색, 삽입, 삭제할 수 있도록 트리를 활용해서 데이터를 구조화하고 인덱싱합니다. 이때 B-트리나 B+트리를 많이 사용해요.

개념

트리는 나무 기둥에서 가지가 뻗어나가는 모습을 거꾸로 뒤집어 놓은 모양의 데이터 구조에요.

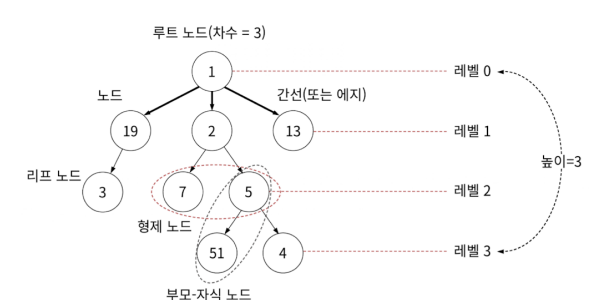
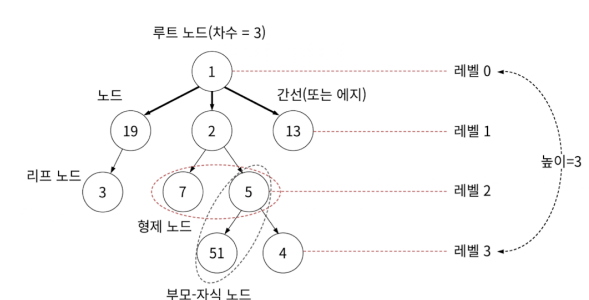다양한 용어들이 존재하는데요. 하나씩 알아봅시다.

구성

트리를 구성하는 노드

노드는 트리를 구성하는 요소이며 가장 위에 있는 노드를 루트 노드라고 해요. 위 그림에서는 1을 값으로 갖고 있는 노드가 루트 노드입니다.

부모-자식, 형제 관계를 가지는 노드

가족 관련된 용어들이 사용되는 경우가 있습니다.

같은 부모 노드를 갖는 노드: 형제 노드
트리에서 특정 노드 아래에 있는 노드가 있다면 특정 노드는 부모 노드, 아래 있는 노드는 자식 노드 라고 해요.

자식이 없는 말단 노드

자식이 없는 노드는 리프 노드라고 해요.

노드를 연결하는 에지

노드와 노드를 이어주는 선을 edge 또는 간선 이라고 합니다.

트리는 노드와 노드가 단방향 간선으로 연결되어 있고 루트 노드에서 각 노드까지 경로는 유일해요.

루트 노드로부터 특정 노드까지 거쳐가는 최소한의 간선 수를 레벨로 표현합니다. ( 루트는 0 그 이후부터 1 2 3 4 ... )

아래로 향하는 간선의 개수, 차수

특정 노드에서 아래로 향하는 간선의 개수를 차수라고 해요. 노드 1은 차수가 3이라고 할 수 있습니다.

이진 트리 구현

모든 노드의 최대 차수가 2를 넘지 않는 트리를 이진 트리 라고 합니다. 구현할 수 있는 방법에는 두 가지가 있어요.

배열을 사용하는 방법
포인터를 사용하는 방법

이진 트리를 구현해보면서 트리랑 좀 더 친해져봅시다.

배열로 구현하기

배열은 선형 자료구조이고 트리는 계층 자료구조입니다. 배열로 트리를 표현하려면 다음 3가지 규칙이 필요해요.

루트 노드는 배열 인덱스 1번에 저장합니다.
왼쪽 자식 노드의 배열 인덱스는 부모 노드의 배열 인덱스 x 2입니다.
오른쪽 자식 노드의 배열 인덱스는 부모 노드의 배열 인덱스 x 2 + 1입니다.

위 규칙에 맞게 구현하면 다음과 같아요.

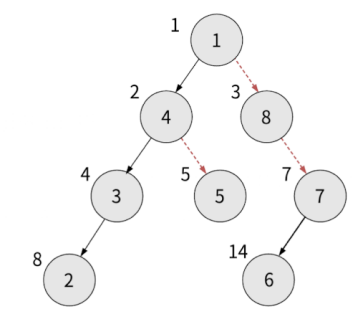
인덱스만 살펴보면 1 2 4 8 이렇게 인덱스가 부모 * 2로 증가합니다. 점선 화살표를 따라가며 인덱스를 확인해보면 1 3 7로 흘러가는 것을 보실 수 있는데요. 부모 * 2 + 1로 증가하는 것을 보실 수 있습니다.

루트 노드를 0으로 설정하면 왼쪽 자식 노드는 부모 * 2 + 1 이고 오른쪽 자식 노드는 부모 * 2 + 2가 됩니다.

배열로 구현하면 되는 것 아닌가 싶으실 수 있는데요. 배열로 구현하면 위 그림에서 14 인덱스를 위해 9 10 11 12 13 인덱스가 비어 있는 것처럼 빈 인덱스가 생기는 상황이 올 수 밖에 없습니다.

이진 트리의 노드가 N개일 때, 배열로 이진 트리를 생성하면 O(N)이 걸립니다.

포인터로 구현하기

포인터로 구현된 트리에서 노드는 노드의 값, 왼쪽 자식 노드, 오른쪽 자식 노드를 가집니다.

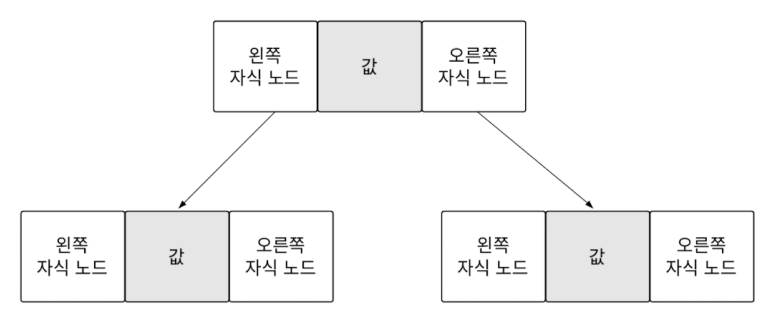
포인터로 구현된 트리는 배열과 달리 인덱스 연산을 하지 않으므로 메모리 공간을 낭비하지 않아요.

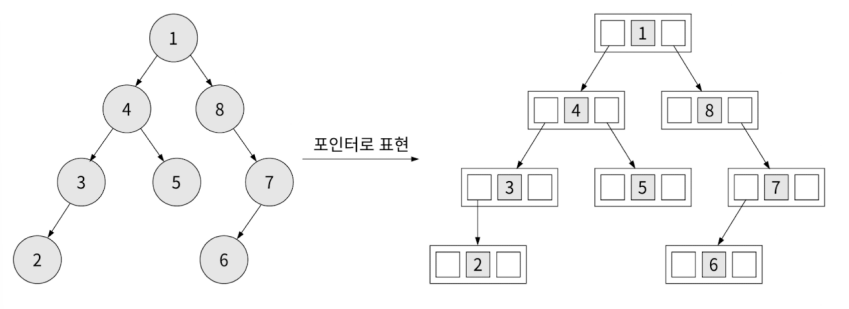
아래 클래스를 통해서 한 노드를 구현하고 left, right 프로퍼티로 연결하는 방식으로 구현해요!

class Node(){
  constructor(value){
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

이진 트리 순회하기

데이터를 위해 특정 자료구조를 빠짐 없이 방문하는 것을 순회라고 하는데요. 배열로 치면 배열의 인덱스로 특정 데이터를 검색할 때 순회가 필요하죠. 트리에서의 순회에는 총 3가지 방법이 있습니다

간단하게 설명해보면 다음과 같아요.

전위 순회 ( Preorder ) : 값 > 왼쪽 자식 > 오른쪽 자식 순서로 방문
중위 순회 ( Inorder ) : 왼쪽 자식 > 값 > 오른쪽 자식 순서로 방문
후위 순회 ( Postorder ) : 왼쪽 자식 > 오른쪽 자식 > 값 순서로 방문 더 자세히 알아봅시다.

전위 순회

현재 노드 > 왼쪽 자식 노드 > 오른쪽 자식 노드 순서로 방문합니다.

방문

탐색에서 방문이란 탐색을 마친 상태를 말합니다. 탐색 과정에서 지나치 는 것과 그렇지 않은 것을 구분하기 위해 방문이라는 용어를 사용합니다. 다음 그림을 보면 한 집은 집 앞을 지나가기만 했고, 나머지 두 집은 방문을 완료했습니다.

아래 배열을 전위 순회한다고 해봅시다.

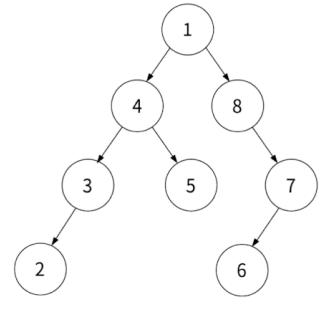
const a = [null, 1, 4, 8, 3, 5, null, 7, 2, null, null, null, 6, null];

인덱스 1부터 루트라고 가정한 트리이므로 그림으로 그리면 다음과 같은데요.

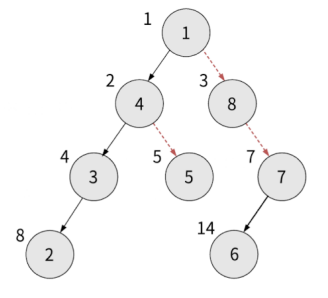
루트 부터 순회를 시작해보자구요. 우선 현재 노드 > 왼쪽 자식 > 오른쪽 자식이기에 루트를 찍고 시작합니다.

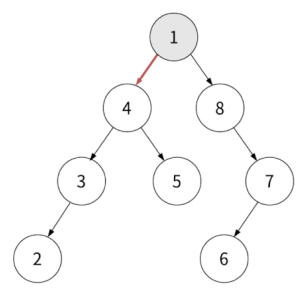반환값: 1

이후 왼쪽 자식 노드로 가서 다시 순회를 돌립니다. 이제 4가 현재 노드가 되었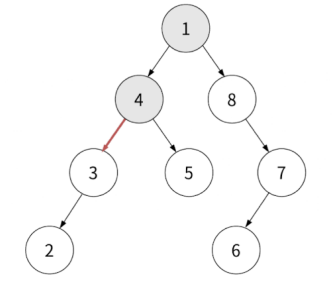어요. 반환값: 1, 4

이 방식으로 똑같이 순회해주다가 자식이 없는 2를 만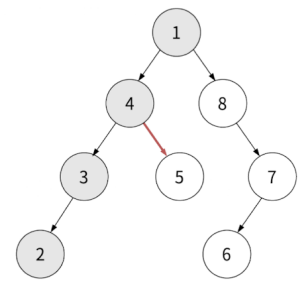나요. 반환값: 1, 4, 3, 2

거슬러 올라가서 가장 최근의 노드중 오른쪽 자식인 5를 순회합니다. 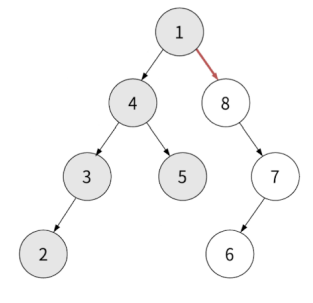반환값: 1, 4, 3, 2, 5

이 방식으로 전체 트리를 순회하면 됩니다. 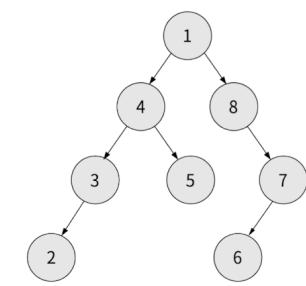반환값: 1, 4, 3, 2, 5, 8, 7, 6

이 방식으로 순회할 경우 현재 노드를 우선 방문(출력)하기 때문에 직관적으로 이해하기 쉬워요. 트리를 복사할 때 많이 사용하는 방식입니다.

중위 순회

왼쪽 자식 노드 > 현재 노드 > 오른쪽 자식 노드 순서로 방문합니다. 현재 노드를 거치기만 하고 왼쪽 노드로 내려가는 방식이에요.

전위 순회랑 똑같은 트리를 순회해볼게요.

값이 1인 루트부터 시작해서 왼쪽 자식의 끝 노드까지 가요. 이때 "방문"하지 않기 때문에 2만 반환됩니다. 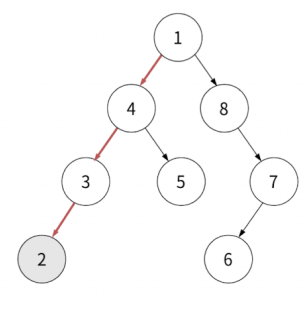반환값: 2

왼쪽 자식 > 현재 노드 > 오른쪽 자식 순서이기 때문에 2 (3의 왼쪽 자식이었던) 에서 거슬러 올라가서 3을 순회합니다. 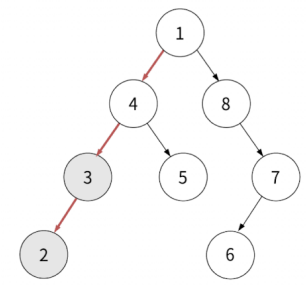반환값: 2, 3

이 방식으로 루트까지 거슬러 올라갑니다. 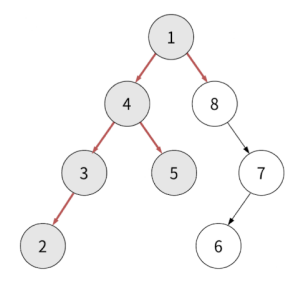반환값: 2, 3, 4, 5, 1

다시 왼쪽 노드, 현재 노드, 오른쪽 노드 방식을 재귀하면서 순회를 완료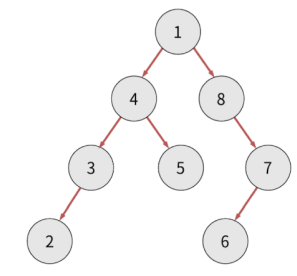해요. 반환값: 2, 3, 4, 5, 1, 8, 6, 7

추가 정보로 이 방식은 뒤에 나올 이진 탐색 트리에서 정렬된 순서대로 값을 가져올 때 활용되니 잘 알아두셔야 합니다.

후위 순회

마지막 순회 방식이에요.

왼쪽 자식 노드 > 오른쪽 자식 노드 > 현재 노드 순서로 방문합니다.

규칙에 따라 중위 순회와 똑같이 왼쪽 자식의 끝으로 가요. 2의 왼쪽 자식, 오른쪽 자식은 없기 때문에 현재 노드인 2를 방문합니다. 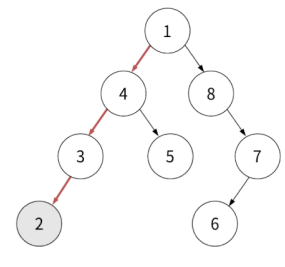반환값: 2

거슬러 올라가는 건 중위순회와 같지만 4에서 조금 바뀝니다. 4는 왼쪽 자식, 오른쪽 자식 둘다 있는 노드에요. 즉 왼쪽 자식인 3이 방문되었다면 다음 순서는 오른쪽 자식이죠. 즉 4 전에 5가 방문됩니다. 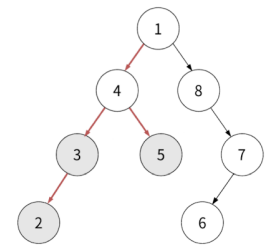반환값: 2, 3, 5

위 현상은 루트에서도 똑같이 일어납니다. 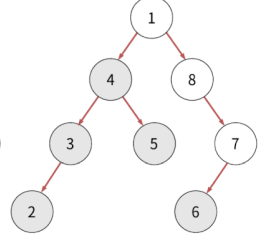반환값: 2, 3, 5, 4, 6

마지막에 루트가 방문되면 순회가 끝나게 됩니다. 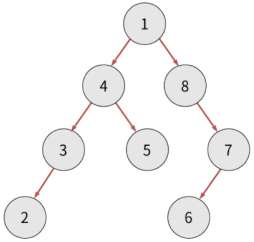반환값: 2, 3, 5, 4, 6, 7, 8, 1

노드를 삭제할 때는 부모를 먼저 삭제하면 안되는데요. 자식 노드부터 삭제해야 트리를 유지하면서 재귀로 루트 노드까지 삭제할 수 있기 때문이죠. 그래서 자식 노드부터 방문한다는 후휘 순회의 특성은 트리 삭제에 자주 활용된다고 해요.

이진 탐색 트리

데이터 크기를 따져서 현재 노드보다 값이 작으면 왼쪽 자식 위치에, 크거나 같으면 오른쪽 자식 위치에 배치하는 독특한 정렬 방식을 가진 이진 트리

이진 트리 탐색하기

트리의 좋은 점은 탐색을 효율적으로 하도록 설계할 수 있다는 것입니다.

자식 노드가 최대 2개인 이진 트리에 특정 규칙을 부여해서 목적에 맞게 사용할 수 있습니다. 그 중 하나인 이진 탐색 트리에 대해서 알아봅시다.

이진 탐색 트리의 규칙은 "데이터 크기를 따져서 현재 노드보다 값이 작으면 왼쪼 자식 위치에, 크거나 같으면 오른쪽 자식 위치에 배치한다." 입니다.

다음의 배열을 이진 탐색 트리에 넣어봅시다.

const arr = [3, 4, 2, 8, 9, 7, 1];

첫 데이터는 루트 노드가 됩니다. 3만이 존재하는 트리가 되요.

이제 이를 기준으로 값이 작으면 왼쪽 값이 크면 오른쪽에 둡니다. 4는 3보다 크니 오른쪽에 둬야 해요.

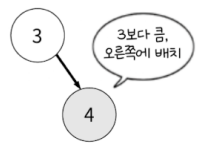
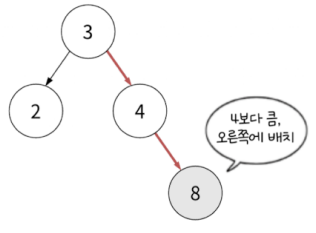
이 방식은 재귀적으로 일어나요. 3, 4, 2 까지는 3을 기준으로 위치가 정해졌다면 8부터는 3 > 4 순서로 규칙이 재귀적으로 적용됩니다. ( 무조건 세번째 값부터라던지 그런 규칙이 아니에요. 3의 두 자식 위치가 다 찼기 때문에 8부터 재귀적으로 적용된겁니다. )

이 방식을 통해 최종적으로 이진 탐색 트리를 완성하면 다음과 같아요.

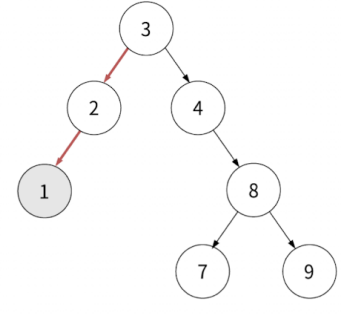
이제 이 트리를 기반으로 탐색을 하면 다음의 순서로 할 수 있어요.

루트부터 시작해서 값이 작으면 왼쪽 자식 노드로, 값이 크면 오른쪽 자식 노드로 이동한다.
특정 값을 찾으면 탐색을 종료한다.

위의 간단한 규칙으로 찾을 수 있어서 굉장히 효율적인 것을 계산하지 않아도 알 수 있겠죠. 자세한 시간 복잡도는 뒤에서 다루겠습니다.

배열 탐색과의 차이

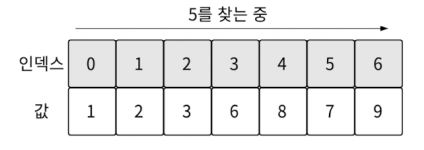
위 상황에서 배열에서는 5를 탐색한다고 했을 때 이를 찾기 위해 7번의 비교 연산이 필요해요. 나올 때까지 배열을 순회해야 하기 때문인데요.

이진 탐색 트리로 같은 상황에서 찾으면 단 2번 만에 탐색이 종료됩니다. ( 탐색하는 인덱스 순서: 0 > 2 > 5, 인덱스 5의 왼쪽 자식이 없으므로 5가 없다는 것을 확인할 수 있어요. )

이진 탐색 트리의 시간 복잡도

이진 탐색 트리의 시간 복잡도는 트리 균형에 의존합니다. 균형이 잡힌 트리는 각 노드의 차수가 비슷하게 유지되면서 각 노드의 자식 노드 수가 비슷하게 유지되는 것을 말하는 데요.

균형이 유지될 경우 가장 이상적이라고 할 수 있습니다. 가장 이상적일 때의 시간 복잡도는 O(logN) 입니다. ( 삽입, 탐색 때 추적 대상이 정확히 반씩 줄어들기 때문이에요. )

반대로 균형이 유지 되지 않았다면 삽입과 탐색 연산 시 O(N) 의 시간복잡도를 가져요. 이는 배열과 일치하죠.

어떤 이유인지 알아봅시다.

비균형적인 트리: 치우쳐진 형태의 트리

degenerate binary tree

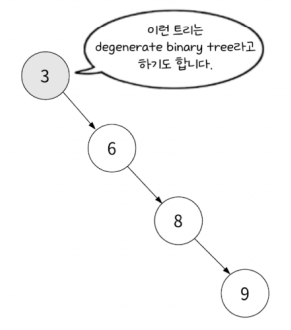
이진 탐색 트리의 규칙은 현재 찾고 싶은 값이 현재 탐색하고 있는 값보다 작으면 그 왼쪽 자식을 탐색하고 아니면 오른쪽 자식, 같으면 탐색을 종료하는 것입니다.

비균형적이면 위 규칙이 필요없는 경우가 많아지겠죠. 한 방향으로만 갈테니까요. 극단적으로 생각하면 이는 배열과 별 다를 게 없는 구조가 됩니다. 즉 시간 복잡도도 배열과 같이 O(N)을 갖는 것이지요.

하지만 이는 수많은 경우 중에 한 경우에요. 만약 위 그림에서 하나라도 루트 노드의 반대쪽 자식으로 이동한다면 배열보다는 성능이 좋다고 할 수 있겠죠.

균형적인 트리: 균형 이진 탐색 트리

균형 이진 탐색 트리는 세부적으로 AVL 트리, 레드-블랙 트리 등으로 구분하여 부르곤 합니다. 이를 활용하면 탐색 연산 횟수가 트리 높이에 비례하고 트리의 높이는 logN이므로 탐색 시간 복잡도를 O(logN)으로 유지할 수 있습니다.

참고 문헌

https://product.kyobobook.co.kr/detail/S000213641007

SUMMARY

알고리즘은 꾸준히 공부해주지 않으면 개념들이 유독 빠르게 사라지는 것 같아요. 사라지면 다시 채워넣을 수 있도록 꾸준히 공부해보겠습니다. 잘못된 지식이 있다면 댓글 부탁드려요!

읽어주셔서 감사해요.

이승현

개념

구성